5.1 관계 대수
- 관계 대수(relational algebra)는 릴레이션을 처리하기 위한 연산(operation)의 집합으로서 각 연산의 피연산자(operand)가 모두 릴레이션이고 연산 결과도 또한 릴레이션이라는 특성을 가지고 있다.
5.1.1 일반 집합 연산자
(1) 합집합(UNION, ∪)
합병 가능한 두 릴레이션 R과 S의 합집합(∪), 즉 R∪S는 릴레이션 R 또는 릴레이션 S에 속하는 튜플 t로 구성되는 릴레이션이다. 수학적 표현을 빌리면 다음과 같이 정의할 수 있다.
R∪S = {t | t∈R ∨ t∈S}
이 합집합으로 만들어진 결과 릴레이션은 두 릴레이션 R이나 S의 차수와 같고 카디널리티 |R∪S| ≤ |R| + |S|가 된다.
(2) 교집합(INTERSECT, ∩)
합병 가능한 두 릴레이션 R과 S의 교집합(∩), 즉 R∩S는 두 릴레이션 R과 S에 공통인, 즉 양 릴레이션에 동시에 속해 있는 튜플 t로만 구성된 릴레이션이다. 식으로 표현하면 다음과 같다
R ∩ S = {t | t∈R ∧ t∈S}
이 교집합으로 만들어지는 결과 릴레이션의 차수는 합집합의 경우와 같은 두 릴레이션 R이나 S의 차수와 같고, 카디널리티 |R ∩ S|는 릴레이션 R이나 S의 어떤 카디널리티보다도 크지 않다. 즉, |R ∩ S| ≤ MIN{ |R|, |S|} 이 된다.
(3) 차집합(DIFFERENCE, -)
합병 가능한 두 릴레이션 R과 S의 차집합(-), 즉 R-S는 릴레이션 R에는 있지만 릴레이션 S에는 없는 튜플 t로만 구성된 릴레이션이다. 식으로 표현하면 다음과 같다.
R - S = {t | t∈R ∧ t!∈S}
이 차집합으로 만들어지는 결과 릴레이션의 차수는 두 릴레이션 R이나 S의 차수와 같고 카디널리티 |R - S|는 릴레이션 R의 카디널리티보다 크지 않다. |R - S| ≤ |R|가 된다.
(4) 카티션 프로덕트(CARTESIAN PRODUCT, ×)
카티션 프로덕트에 관계된 릴레이션들은 서로 합병 가능한 릴레이션이 되어야만 하는 것은 아니다. 두 릴레이션 R(A1, A2, ..., An)과 S(B1, B2, ..., Bm)의 카티션 프로덕트(×), 즉 R×S는 R에 속한 각 튜플 r에 대해 릴레이션 S에 속한 각 튜플 s를 모두 접속(concatenation ; ·)시킨 튜플 r·s로 구성된 릴레이션이다. 이 카티션 프로덕트를 식으로 표현하면 다음과 같다.
R × S = {r·s | r∈R ∧ s∈S}
5.1.2 순수 관계 연산자
(1) 실렉트(SELECT)
이 실렉트 연산은 σ(sigma)로 표현한다. 이 연산은 기본적으로 릴레이션에서 주어진 조건을 만족하는 튜플들을 선택하는 연산이다. A와 B를 릴레이션 R의 애트리뷰트로, θ는 비교 연산자(=, ≠, <, ≤, >, ≥), v는 상수라고 하자. 애트리뷰트 A와 B에 대한 릴레이션 R의 실렉트 연산은 다음과 같다.
① σAθv(R) = {r | r∈R ∧ r.Aθv}
② σAθB(R) = {r | r∈R ∧ r.Aθr.B}
- 릴레이션은 주어진 릴레이션을 수평적으로 절단하여 그 일부를 가지고 구성한 것과 같으므로 실렉트는 수평적 부분 집합(horizontal subset)을 생성한다고 볼 수 있다.
- 실렉트의 수학적 표현을 사용자가 사용하는 데이터 언어에서는 보통 선택 조건을 명세하는 WHERE 절로 나타내고 있다. R WHERE 조건식
- 선택 조건에 의해 선택되는 튜플과 릴레이션 전체 튜플의 비율을 그 선택 조건의 선택도(selectivity)라 한다.

(2) 프로젝트(PROJECT, Π)
- 릴레이션을 수직적으로 절단한 열(column)의 집합으로 보면 결과 릴레이션은 주어진 릴레잉션의 몇몇 열들로 구성한 것이기 때문에 프로젝트는 릴레이션의 수직적 부분 집합(vertical subset)이라 볼 수 있다.

(3) 조인(JOIN)

- 여기서 θ는 조인 조건에 사용되는 비교 연산자이고 A와 B는 같은 도메인 위에 정의된 조인 애트리뷰트(join attribute)라 한다.
- 릴레이션의 차수는 릴레이션 R의 차수와 S의 차수를 합한 것과 같다. 결과가 릴레이션의 각 애트리뷰트는 유일성을 만족시켜야 되는데 보통 원 소속 릴레이션의 이름을 애트리뷰트 앞에 한정어로 붙여 유일성을 유지한다.
- 조인의 정의에서 볼 수 있는 것과 같이 비교 연산자는 θ(theta)로 표현하여 일반화하였는데 이 θ로 표현될 수 있는 조인을 세타 조인(θ-join, theta join)이라고 한다.

- θ가 "="인 조인을 동일 조인(equijoin)이라 한다.

- 동일 조인 결과 릴레이션에서 중복되는 애트리뷰트를 제거할 필요성이 있게 되는데 이렇게 해주는 연산이 자연 조인(natrual join)이다.
- 보통 조인이라고 하면 이 자연 조인을 말하는데 특별히 이 자연 조인을 표현하기 위한 연산 기호로 ⋈N 을 사용한다.
- 자연 조인은 다음과 같이 정의된다.

(4) 디비전(DIVISION, ÷)
- 두 릴레이션 R(X)와 S(Y)에 대해 Y⊆X이고 X-Y=D라고 하자. 그러면 R(X) = R(D, Y)로 표현할 수 있다.
- 이것을 공식적으로 정의하면 다음과 같다.

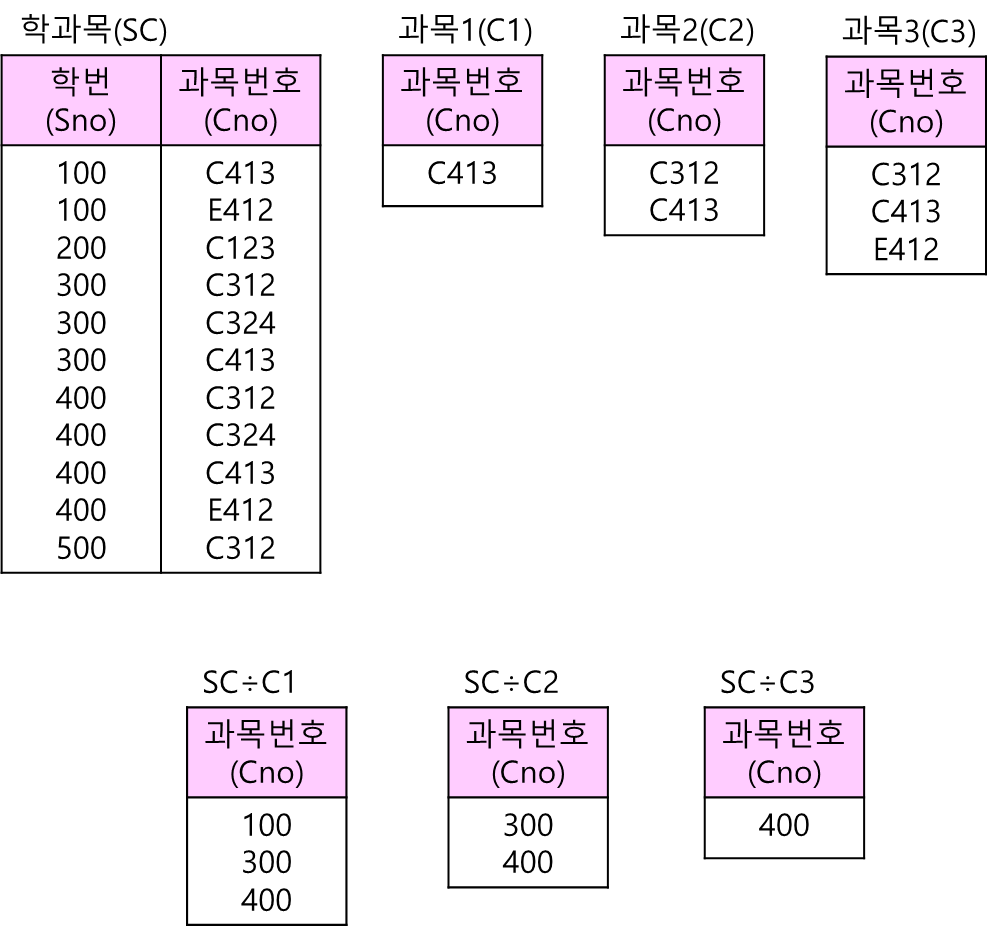
5.1.3 기본 연산과 복합 연산
- 합집합, 차집합, 카티션 프로덕트, 실렉트, 프로젝트 연살은 기본 연산(primitive operation)이라 하고, 그 이외의 조인, 교집합, 디비전 연산을 복합 연산(composite operation)이라 한다.
- 기본 연산과 복합 연산의 차이는 기본 연산은 하나의 논리적 기능을 수행하는 연산으로 다른 연산을 이용하여 대체할 수 없는 연산이고 복합 연산은 앞에 열거한 5개의 기본 연산을 이용하여 그 연산의 기능을 대체할 수 있다는 점이 다르다.
5.1.4 관계 대수의 확장
(1) 세미 조인과 외부 조인
릴레이션 R(X)에 대해 S(Y)의 세미 조인(semijoin)은 R⋉S로 표현하며 그 정의는 다음과 같다.

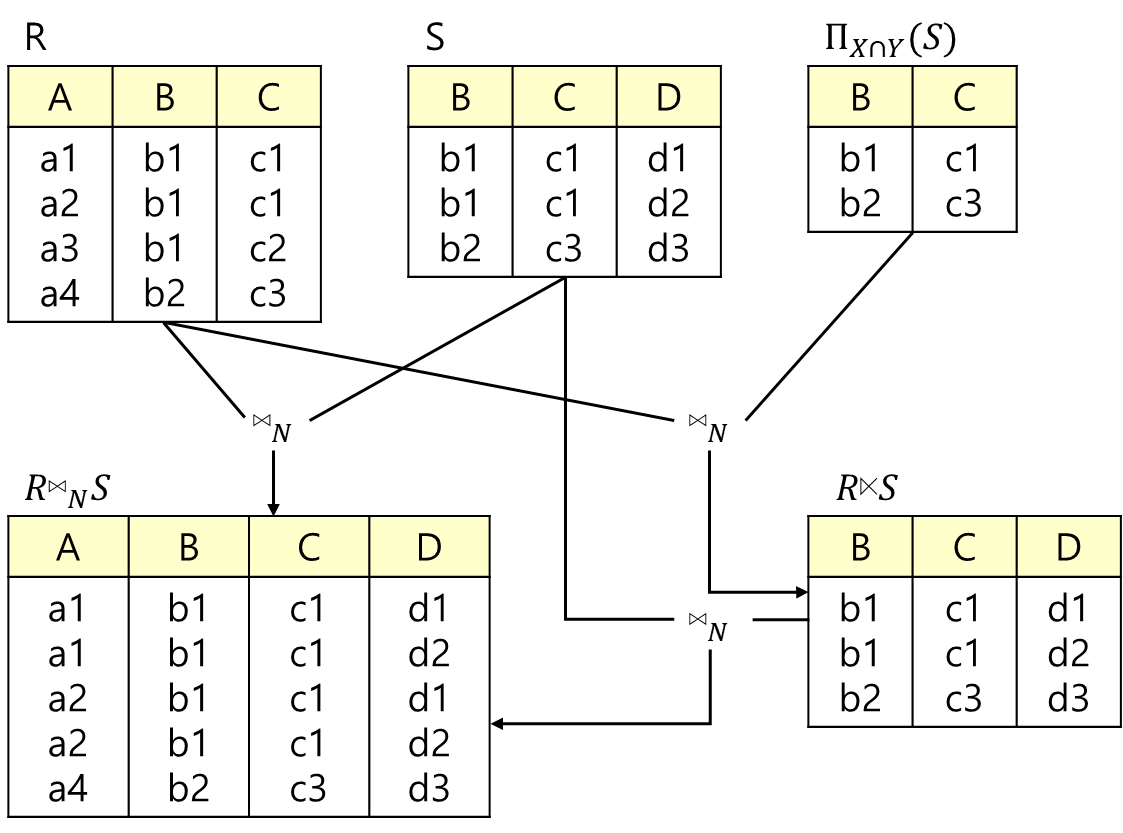
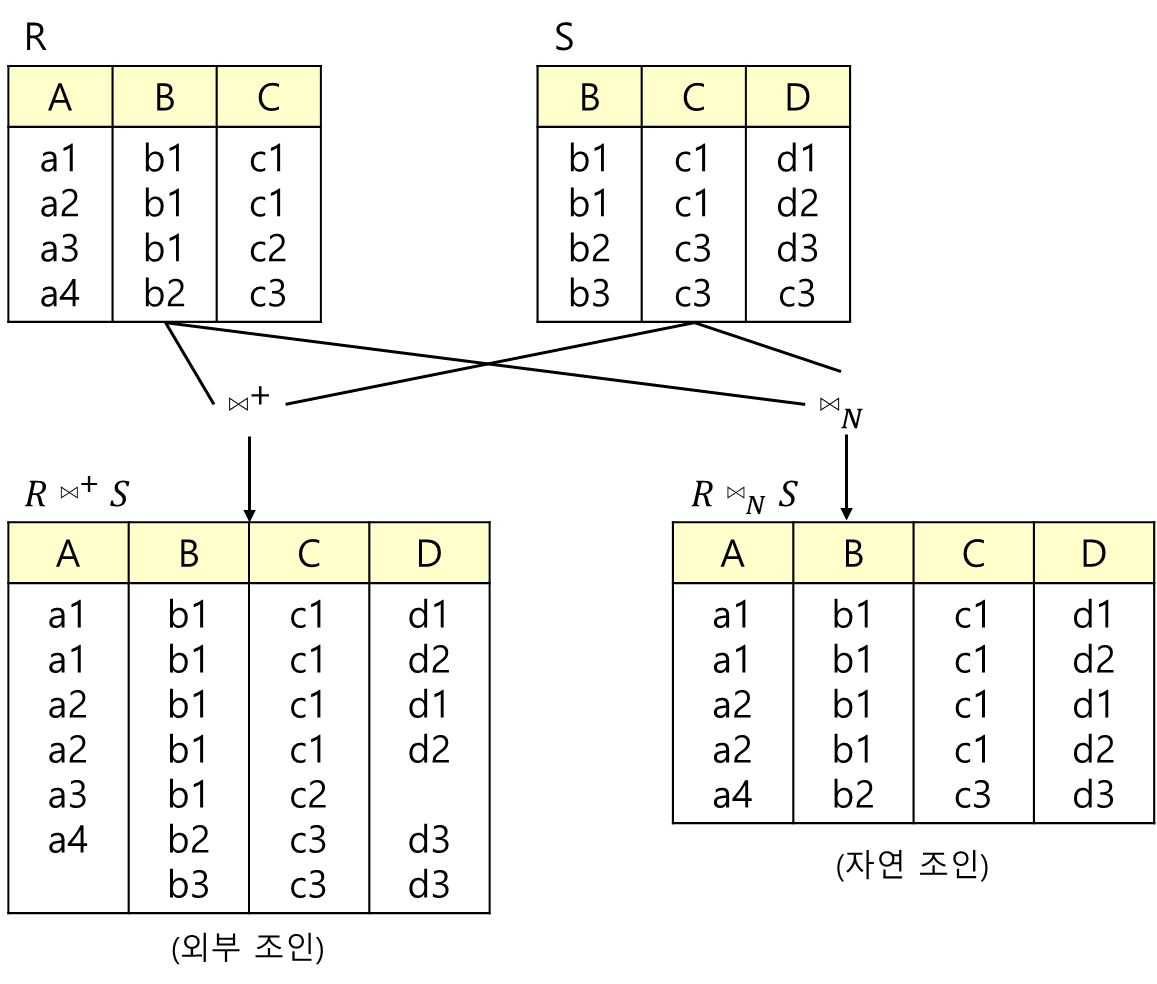
- 외부 조인(outerjoin)은 보통의 조인, 즉 내부 조인(innerjoin)을 확장한 개념이다.
- 즉, 조인을 하는 과정에서 한 릴레있는 어떤 튜플이 조인할 상대 릴레이션에 대응되는 튜플이 없을 경우에 이를 제외시키지 않고 상대를 널(null) 튜플로 만들어 결과 릴레이션에 포함시키는 연산이다.
- 외부 조인을 수행하면 두 릴레이션에 있는 튜플들이 전부 결과 릴레이션에 포함되게 된다.
(2) 외부 합집합(outer-union, ∪+)
- 외부 합집합(outer-union) ∪+는 완전하게 합병 가능하지 않은 두 릴레이션을 합집합으로 만드는 것이다.
- 확장된 애트리뷰트에 해당되는 값이 없는 튜플들은 널(공백) 값으로 채워지게 된다.

(3) 집계 연산
- 이 연산에는 애트리뷰트 값의 집합에 대해 적용할 수 있는 수학적인 집계 함수(aggregate function)으로서 SUM, AVG, MAX, MIN, COUNT 등이 있다.
- SUM은 집합에 있는 값들의 합계를 계산하고, AVG는 집합에 있는 값들의 평균값을 계산하며 MAX와 MIN은 집합에 있는 값 중에서 최대 값과 최소 값을 계산한다. 그리고 COUNT는 집합 속에 있는 값들의 개수를 계산한다.
- 집계 함수 이외에 특별히 지정한 애트리뷰트 값에 따라 튜플들을 그룹 짓게 하는 그룹핑 함수(grouping function) GROUP이 있다.
5.2 관계 해석
5.2.1 튜플 관계 해석
(1) 튜플 변수
- 튜플 변수(tuple variable)는 범위 변수(range variable)라고도 하는데 이것은 지정된 릴레이션의 튜플을 하나 씩 그 값을 취할 수 있는 변수이다.
- 튜플 변수는 그것이 튜플을 값으로 취할 수 있는 범위로 명세된 릴레이션을 가지게 된다.
- R(t)를 튜플 변수 t의 범위 식(range formula)이라 하고 R을 t의 범위 릴레이션(range relation)이라 한다.
(2) 한정 애트리뷰트
- 릴레이션 R에 대해 튜플 변수 t가 나타내는 튜플의 어떤 애트리뷰트 A의 값을 표현하기 위해서는 t.A 또는 t[A]로 표기한다. 이때 t.A를 한정 애트리뷰트(qualified attribute)라 한다.
(3) 원자식
- 범위식, R(t), 여기서 t는 튜플 변수이고 R은 t의 범위 릴레이션이다.
- 조건식, t.Aθu.B, 여기서 t와 u는 튜플 변수이고 A와 B는 각각 t와 u에 대한 한정 애트리뷰트이다. θ는 비교 연산자로서 =, ≠, <, ≤, >, ≥을 말한다.
- 조건식, t.Aθc, 여기서 A는 튜플 변수 t에 대한 한정 애트리뷰트이고, c는 상수이다. 이 원자식을 실행한 결과는 항상 참(true) 값이나 거짓(false)값을 갖는다.
(4) 정형식
원자식, 불리언 연산자(boolean operator)인 ∧, ∨, ¬, 그리고 정량자(quantifier)인 ∃(there exists), ∀(for all)이 다음과 같은 규칙에 따라 결합된 식을 정형식(WFF : Well Formed Formula)이라 하고 'weff'라 읽는다.
- 모든 원자식은 WFF이다.
- F가 WFF이면 (F)와 ¬F도 WFF이다.
- F와 G가 WFF이면 F∧G와 F∨G도 WFF이다.
- 튜플 변수 t가 자유 변수로 사용된 F(t)가 WFF이면 (∃t)(F(t))와 (∀t)(F(t))도 WFF이다. 여기서 자유 변수(free variable)란 정량자(∃, ∀)로 한정되지 않은 튜플 변수를 말한다. 만일 정량자로 한정되었다면 속박 변수(bound variable)라 한다. 정량자 ∃는 존재 정량자(existential quantifier)라고 하며 "there exists"라 읽는다. 정형식, (∃t)(F(t))에서 만일 정형식 F(t)를 참(true)으로 만드는 어떤 튜플 t가 있을 때 이 (∃t)(F(t))는 참(true)으로 된다. 이것은 정형식 F(t)를 참으로 만드는 변수 t에 지정할 튜플이 적어도 하나 존재한다라는 뜻이다. 정량자 ∀은 전칭 정량자(universal qantifier)로 "for all"이라 읽는다. 정형식 (∀t)(F(t))에서 모든 가능한 튜플 t에 대해 정형식 F(t)가 참(true)이 될 때 (∀t)(F(t))는 참이 된다. 즉 이것은 변수에 지정하는 모든 튜플에 대해 정형식 F(t)가 참이 된다는 뜻이다.
- 위 1 ~ 4의 규칙만을 적용해서 만들어진 식은 WFF이다.
- 정량자가 사용된 논리식에서 정량자를 모두 앞으로 먼저 기술하는 방법이 있다. 이것을 프리닉스 정규형(prenex normal form)이라 한다.
5.2.3 도메인 관계 해석
(1) 도메인 변수
- 도메인 변수(domain variable)는 언제 어느 때라도 지정된 애트리뷰트의 도메인의 한 원소만을 값으로 취하는 변수이다.
(2) 원자식
- 범위식, R(x1, x2, ..., xn), 여기서 xi는 도메인 변수이고 R은 xi의 범위 릴레이션이다. 이 원자식은 도메인 변수 리스트<x1, x2, ..., xn>에 해당하는 값의 리스트는 릴레이션 R의 튜플이어야 한다는 것을 의미한다.
- 조건식, xθy, 여기서 x와 y는 도메인 변수이고 θ는 비교 연산자(=, ≠, <, ≤, >, ≥)이다.
- 조건식, xθc, 여기서 x는 도메인 변수이고 θ는 비교 연산자이며 c는 x가 정의된 도메인 값의 상수이다.
이 원자식을 실행한 결과를 반드시 참(true)값이나 거짓(false)이 된다.
(3) 정형식
원자식, 불리언 연산자인 ∧, ∨, ¬, 그리고 정량자인 ∃(there exists), ∀(for all)이 다음과 같은 규칙에 따라 결합되어 표현된 식을 정형식(WFF : Well Formed Formula)이라 한다.
- 모든 원자식은 WFF이다.
- F가 WFF이면 (F)와 ¬F도 WFF이다.
- F와 G가 WFF이면 F∧G와 F∨G도 WFF이다.
- 도메인 변수 x가 자유 변수로 사용된 F(x)가 WFF이면 (∃x)(F(x))와 (∀x)(F(x))도 WFF이다. 여기서 자유 변수란 정량자 ∃(there exists)나 ∀(for all)로 한정되지 않은 도메인 변수를 말한다.
- 위의 규칙만을 반복적으로 적용해서 만들어진 식은 WFF이다.
'임용 > 데이터베이스' 카테고리의 다른 글
| Chapter 07 데이터 종속성과 정규화 (0) | 2023.04.18 |
|---|---|
| Chapter 06 SQL (0) | 2023.04.17 |
| Chapter 04 관계 데이터베이스 (0) | 2023.04.12 |
| Chapter 03 데이터베이스 시스템의 구성 (0) | 2023.04.12 |
| Chapter 02 데이터베이스 관리 시스템 (0) | 2023.04.11 |